Тема 2. Свойства дисперсных систем,
Их устойчивость и коагуляция
Электрические свойства дисперсных систем
1. Электрокинетический потенциал.
2. Теории строения двойного электрического слоя.
1. Щукин Е.Д., Перцов А.В., Амелина Е.А. Коллоидная химия. – М.: Высш. шк., 2006. – С. 139 – 154, 172 – 190.
2. Гельфман М.И., Ковалевич О.В., Юстратов В.П. Коллоидная химия. – СПб.: «Лань», 2003. – С. 106 – 116.
НАГЛЯДНЫЕ ПОСОБИЯ И ПРИЛОЖЕНИЯ:
1. Cвойства дисперсных систем.
2. ДЭС по теории Гельмольца-Перрена.
3.. ДЭС по теории Гуи-Чэпмена.
5. Факторы, влияющие на дзета-потенциал.
6. Электрокинетический потенциал.
Мы продолжаем изучение темы № 2 «Свойств дисперсных систем, их устойчивость и коагуляция». На прошлых лекциях были рассмотрены молекулярно-кинетические, оптические, а также электрические свойства дисперсных систем, которые проявляются в виде электрокинетических явлений (рисунок 1).
Рис. 1. Свойства дисперсных систем
Сегодня мы продолжим рассмотрение электрических свойств, ознакомимся с понятием электрокинетический потенциал, детально рассмотрим строение двойного электрического слоя и, как следствие, изучим строение коллоидной мицеллы. Материал сегодняшней лекции является основополагающим для рассмотрения вопроса устойчивости дисперсных систем и их разрушения – одного из центральных вопросов физики поверхности.
ЭЛЕКТРОКИНЕТИЧЕСКИЙ ПОТЕНЦИАЛ
Как мы показали на прошлой лекции на частицах дисперсной фазы, помещенных в жидкую дисперсионную среду, практически всегда возникает заряд (рисунок 2).
1.Избыток КСI 2. Избыток AgNO3
Рисунок 2. Возникновение заряда на поверхности частиц
Возникновение заряда на поверхности твердого тела приводит к тому, что на границе раздела фаз (между твердой частицей и раствором) возникает электрический потенциал. Его обозначают через j и называют термодинамическим или электрохимическим потенциалом. Ионы, из-за которых на поверхности частиц возникает заряд, называются потенциалобразующими (или потенциалопределяющими).
Однако в электрокинетических явлениях проявляется потенциал меньше, чем термодинамический. Электрокинетическим или дзета-потенциалом называют потенциал, который проявляется на границе скольжения при перемещении частиц дисперсной фазы относительно дисперсионной среды (например, в электрическом поле). Его обозначают буквой z (дзета). Было установлено, что частица дисперсной фазы при движении увлекает за собой часть жидкости, которая перемещается вместе с частицей, и z- потенциал возникает на границе скольжения. Граница скольжения отделяет неподвижную, связанную с твердой частицей жидкую фазу от остальной жидкой фазы, относительно которой происходит перемещение дисперсных частиц (рисунок 3).
 |
Рис. 3. Граница скольжения между дисперсной частицей
(вместе с прилегающим слоем) и дисперсионной средой
Расстояние от поверхности частицы до границы скольжения определяется в первую очередь вязкостью дисперсионной среды. Таким образом, термодинамический потенциал возникает на границе между частицей и дисперсионной средой, а электрокинетический — на границе скольжения.
Электрокинетический потенциал – важная характеристика дисперсной системы. Он определяет скорость перемещения дисперсной фазы и дисперсионной среды, интенсивность электрокинетических явлений, устойчивость золей и разрушение их электролитами. Величину электрокинетического потенциала можно достаточно точно измерить по данным электрофореза или электроосмоса. Его знак определяется знаком заряда потенциалопределяющего слоя: если слой формируется анионами, то z- потенциал будет отрицательным, если он образуется из катионов, то отрицательным.
1. Расчет z- потенциала по данным электрофореза.

где u – скорость перемещения частиц дисперсной фазы, м/с
(можно наблюдать визуально и измерить);
h – коэффициент вязкости среды, н . с/ м 2 ;
y – коэффициент, учитывающий форму частиц (для сферических –
0,66; для цилиндрических – 1);
e – относительная диэлектрическая проницаемость среды;
eо – абсолютная диэлектрическая проницаемость вакуума
Е – напряженность внешнего электрического поля, В/м.
Таким образом, электрокинетический потенциал довольно просто определить экспериментально по скорости перемещения дисперсной фазы в электрическом поле с известным значением напряженности. Электрокинетический потенциал обычно не превышает 100 мВ.
2. Расчет z- потенциала по данным электроосмоса.

где Q – oбъемная скорость электроосмоса, м 3 /с
(объем раствора, протекающего через пористую мембрану
h – коэффициент вязкости среды, н . с/ м 2 ;
c – удельная электропроводность, См/м;
e – относительная диэлектрическая проницаемость среды;
eо – абсолютная диэлектрическая проницаемость вакуума
I – сила тока, при которой проводился осмос, А.
Таким образом, чтобы определить величину электрокинетического потенциала z по данным электроосмоса надо экспериментально определить объем жидкости, перенесенной через пористую мембрану, удельную электропроводность раствора и силу тока, при которой проводился электроосмос.
Величина электрокинетического потенциала влияет на устойчивость дисперсных систем, на скорость электрофореза и электроосмоса. Величину z- потенциала можно изменить в соответствии с поставленными целями. Для этого необходимо знать факторы, влияющие на z- потенциал.
Факторы, влияющие на z- потенциал
1. Величина термодинамического потенциала j (чем больше j, тем больше z);
2. Концентрация индифферентного электролита в растворе (z- потенциал может сильно уменьшиться, даже до 0, или переменить знак на противоположный);
3. рН раствора (в некоторых случаях).
Чтобы понять причины влияния этих факторов на z- потенциал, необходимо рассмотреть строение двойного электрического слоя.
источник
На поверхности частиц дисперсных фазы при их контакте с жидкостью самопроизвольно возникает избыточный электрический заряд и формируется потенциалобразующий слой ионов (см. тему 3). К твердой поверхности из жидкой среды притягиваются ионы, знак которых противоположен знаку потенциалобразующего слоя. Они называются противоионами. Возникает двойной электрический слой (ДЭС). Его можно рассматривать как своеобразный конденсатор, внутренняя обкладка которого формируется из потенциалобразующего слоя ионов, а внешняя – из противоионов. Противоионы находятся в двух положениях: одна их часть образует адсорбционный слой, другая находится в диффузном слое.
Потенциал, возникающий на поверхности коллоидной частицы, называют электрокинетическим или ζ (дзета) – потенциалом. Электрокинетический потенциал численно равен работе, которую нужно совершить при переносе единицы заряда с поверхности гранулы в глубь дисперсной среды или наоборот.
Электрический заряд может возникать на любой твердой поверхности, находящейся в контакте с жидкостью. Наличие заряда на поверхности коллоидных частиц является причиной возникновения электрокинетических явлений, характерных только для дисперсных систем. Электрокинетическими называют такие явления, которые возникают при воздействии электрического поля на дисперсные системы и в результате перемещения частиц дисперсной фазы и дисперсной среды.
Внешнее электрическое поле вызывает такие электрокинетические явления, как электрофорез и электроосмос. Электрофорез – это перемещение дисперсной фазы относительно дисперсной среды в электрическом поле. Электроосмос – перемещение дисперсной среды относительно дисперсной фазы под действием внешнего электрического поля. При электрофорезе коллоидные частицы движутся к одному электроду, а диффузный слой противоионов перемещается к другому электроду. Измеряя скорость электрофореза и электроосмоса, можно определить электрокинетический потенциал. Зависимость скорости перемещения фаз от электрокинетического потенциала описывается уравнением Гельмгольца-Смолуховского:
(17),
U – скорость перемещения фазы,
ζ – электрокинетический потенциал,
E – напряженность или градиент внешнего поля,
η – вязкость дисперсионной среды,
ε – диэлектрическая проницаемость среды,
ε – электрическая постоянная или абсолютная диэлектрическая проницаемость вакуума, равная .
При электрофорезе скорость движения частиц U при напряженности электрического поля Е, равной единице, называют электрофоретической подвижностью Иэф, , то есть:
(18)
Электрокинетический потенциал можно рассчитать по формулам:
(19),
(20),
Электрокинетический потенциал является важным фактором устойчивости коллоидных систем.
Рассмотрим решение типовой задачи.
Задача 4.1. определите электрокинетический потенциал 20%-ного коллоидного раствора сахарозы при градиенте внешнего электрического поля 400 В/м, относительной диэлектрической проницаемости 69,4 , вязкости . Скорость электрофореза равна 13,5 мкм/с.
Решение: электрокинетический потенциал рассчитывается по формуле (19):
Ответ:электрокинетический потенциал равен 82,4мВ.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
источник
Электрокинетический (дзета) потенциал – потенциал, возникающий на границе скольжения фаз при их относительном перемещении в электрическом поле.
Положение плоскости скольжения (линия АВ) в ДЭС не известно. Полагают, что плоскость скольжения проходит на расстоянии толщины плотной части ДЭС, и в этом случае ζ = φd; либо смещена в жидкую фазу, тогдаζ 2 /В·с; U – линейная скорость движения границы золь – боковая жидкость, м/с; H – напряженность электрического поля, В/м.
Электрокинетический потенциал связан с электрофоретической (электроосмотической) подвижностью, уравнением Гельмгольца – Смолуховского:
, (4.3)
где ζ – величина электрокинетического потенциала, В; η – вязкость дисперсионной среды, Н·с/м 2 ; ε – диэлектрическая проницаемость среды, для водной среды равная 81 (безразмерная величина); – электрическая константа (диэлектрическая проницаемость вакуума), равная 8,85·10 –12 Ф/м; U – линейная скорость движения границы золь-боковая жидкость, м/с; H – напряженность электрического поля, В/м.
Линейную скорость движения границы золь-боковая жидкость рассчитывают как отношение смещения границы раздела за время электрофореза:
, (4.4)
где h – смещение границы золь-боковая жидкость за время электрофореза, м; t – время электрофореза, с.
Напряженность электрического поля (градиент потенциала) рассчитывают как отношение приложенной разности потенциалов к расстоянию между электродами:
, (4.5)
где Е – приложенная разность потенциалов, В; l – расстояние между электродами, м.
Тогда уравнение Гельмгольца – Смолуховского для электрофорезазапишется:
. (4.6)
Расчет электрокинетического потенциала при электроосмосе ведут по уравнению:
, (4.7)
где – величина электрокинетического потенциала, В; – вязкость среды, Н·с/м 2 ; – диэлектрическая проницаемость среды, для водной среды равная 81 (безразмерная величина); – электрическая константа (диэлектрическая проницаемость вакуума), равная 8,85·10 –12 Ф/м;
– удельная электрическая проводимость, Ом –1 м –1 ; – объемная скорость электроосмоса, м 3 /с; I – сила тока, А.
Объемная скорость электроосмоса ( ) – скорость перемещения объема раствора V,(м 3 ) в единицу времени t, с:
. (4.8)
Потенциал течения – возникновение разности потенциалов при продавливании через пористую диафрагму жидкости под действием внешней силы (давления).
Потенциал течения не зависит от площади и толщины диафрагмы, от количества протекающей жидкости, а зависит от давления, поддерживающего течение по уравнению:
, (4.9)
где – потенциал течения, В; – величина электрокинетического потенциала, В; – вязкость среды, Н·с/м 2 ; – диэлектрическая проницаемость среды, для водной среды равная 81 (безразмерная величина); – электрическая константа (диэлектрическая проницаемость вакуума), равная 8,85·10 –12 Ф/м; – удельная электрическая проводимость, Ом –1 м –1 ; р – давление, приводящее жидкость в движение, Н/м 2 .
Пример 4.1.Вычислите величину электрокинетического потенциала для латекса полистирола, если при электрофорезе смещение цветной границы за 60 мин составляет h = 2,6 см. Напряжение, приложенное
в электродам Е = 115 В. Расстояние между электродами l = 55 см. Диэлектрическая проницаемость воды ε = 81, вязкость среды η = 1·10 –3 Н·с/м 2 .
Решение. Для расчета электрокинетического потенциала воспользуемся уравнением (4.6):
.
Не нашли то, что искали? Воспользуйтесь поиском:
источник
Согласно современной теории строения двойного электрического слоя получили объяснение электрические явления, а также проблемы строения и устойчивости коллоидных частиц лиофобных золей. Установлено, что при относительном движении жидкой и твердой фаз в электрическом поле плоскость скольжения их лежит на некотором расстоянии от твердой фазы. При этом слой жидкой фазы толщиной в 2-3 молекулы при движении фаз остается неподвижным вместе с твердой фазой. Иными словами, непосредственно у поверхности коллоидной частицы образуется адсорбционный слой, включающий не только ПОИ, но и часть противоионов, которые в обычных условиях считаются неподвижными и при движении твердой фазы перемещаются вместе с ней. Остальная часть противоионов составляет диффузный слой, в котором концентрация ионов по мере удаления от поверхности коллоидной частицы постепенно убывает. Между адсорбционным и диффузным слоями идет непрерывный обмен противоионами.
Разность потенциалов между подвижной (диффузной) и неподвижной (адсорбционной) частями двойного электрического слоя называется электрокинетическим потенциалом. Этот потенциал обозначается греческой буквой ζ(дзетта) и потому называется дзетта-потенциалом (ζ-потенциал).
Полное падение потенциала от его значения на твердой поверхности (заряженной отрицательно) до минимального значения соответствует максимальной разности потенциалов между твердой поверхностью и всеми вместе взятыми противоионами. Эту максимальную разность потенциалов называют термодинамическим потенциалом y (рис. 20.3). ζ-потенциал или электрокинетический потенциал составляет часть термодинамического потенциала y и показывает скачок потенциала в диффузной части двойного электрического слоя.
Рис. 20.4 Схема строения ДЭС и кривая падения потенциала
(металл заряжен отрицательно)
Вычисление электрокинетического потенциала ζ определение его знака на практике производят, пользуясь данными электрофореза и электроосмоса, а также потенциала течения, по следующей формуле:
(20.1)
где К – постоянная, зависящая от формы коллоидно-дисперсных частиц (для сферических частиц К=6, цилиндрических – К=4),
h – вязкость дисперсионной среды,
D – диэлектрическая постоянная,
e – градиент напряжения поля,
u – средняя скорость передвижения частиц под действием электрического поля.
Установлено, что величина ζ-потенциала тесно связана с толщиной диффузного слоя противоионов. Чем больше размыт этот слой, тем больше величина электрокинетического потенциала.
Если слой противоионов предельно сжат, ζ-потенциал = 0. Наоборот, разбавление золя способствует увеличению толщины диффузного слоя за счет перехода противоионов из адсорбционного в диффузный слой и приводит к возрастанию значения ζ-потенциала.
Так как ζ-потенциал в некоторых случаях является величиной, характеризующей устойчивость коллоидной системы, необходимо учитывать влияние на него таких факторов, как введение в систему электролитов, изменение pH, концентрации раствора, температуры и т.д.
Индифферентные электролиты (электролиты, не имеющие ионов, способных достраивать кристаллическую решетку коллоидной системы) не могут существенно изменить общий скачок потенциала коллоидных частиц, а электрокинетический потенциал снижается в результате увеличения концентрации противоионов и сжатия двойного электрического слоя.
При введении в коллоидный раствор индифферентных электролитов различают два случая:
1) в систему вводится электролит, один из ионов которого одинаков с противоионами;
2) в систему вводится электролит, не имеющий общих ионов с электролитом – стабилизатором.
В первом случае по мере увеличении содержания в системе такого электролита, очевидно, толщина двойного электрического слоя стремится стать равной толщине адсорбционного слоя за счет сжатия диффузного слоя. В результате электрокинетический потенциал понижается, пока не станет равным 0, что будет отвечать так называемому изоэлектрическому состоянию системы.
Второй случай отличается от первого только тем, что здесь имеет место явление обмена противоионов коллоидной частицы на эквивалентное число одинаковых по знаку ионов введенного электролита.
Значение pH дисперсионной среды может сильно сказываться на электрокинетическом потенциале коллоидных частиц, т.к. водородные и гидроксильные ионы обладают высокой способностью адсорбироваться; первые – благодаря малому радиусу, что позволяет им близко подходить к поверхности твердой фазы; вторые – из-за большого дипольного момента.
Дата добавления: 2014-01-07 ; Просмотров: 3226 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
источник
При подготовке к лабораторной работе повторите материалы гл. 5, обратив особое внимание на параграф 5.2.
Цель работы. Определение электрокинетического потенциала золя берлинской лазури по скорости электрофореза.
Реактивы и оборудование. Растворы для приготовления золя: K4[Fe(CN)6] нас., FeCl3nac., NaCl 0,01 М, дистиллированная вода.
Установка для определения ^-потенциала золей методом электрофореза (методом подвижной границы), источник постоянного тока, линейка, секундомер, стакан химический мерный объемом 500 мл, пипетка мерная объемом 1 мл, резиновая груша, стеклянная палочка.
Методические указания. В лаборатории для определения ^-потенциала золей методом электрофореза используют установку, показанную на рис. Л.4.
В нижнюю часть U-образной трубки заливают окрашенный золь (например, золь берлинской лазури), сверху — воду, так чтобы между золем и водой была отчетливая ровная граница. При включении напряжения окрашенные частицы твердой фазы золя начнут сдвигаться в сторону одного из электродов в зависимости от знака заряда коллоидной частицы. Скорость сдвига зависит от величины электрокинетического потенциала коллоидной частицы, напряженности электрического поля, вязкости и диэлектрической проницаемости среды.
Рис. Л.4. Установка для определения ^-потенциала методом электрофореза
Заполнение прибора проводят в следующей последовательности:
- 1) в U-образную трубку залить дистиллированную воду примерно на 1 /3 объема;
- 2) соединяющийся с трубкой сосуд наполнить изучаемым окрашенным золем до самого верха;
- 3) медленно открывая кран между U-образной трубкой и сосудом, выпустить пузырьки воздуха, который мог остаться в месте соединения, а затем заполнить нижнюю часть U-образной трубки золем. При этом имеющаяся в трубке вода поднимется вверх, а между водой и золем образуется четкая граница раздела.
Электроды погружают в воду, как показано на рис. Л.4, они не должны доходить до границы золя на несколько сантиметров.
Проведение измерений. Отметив положение границы в обоих коленах, подключают напряжение. Электрофорез проводят на постоянном токе с напряжением 20—30 В (регулируется с помощью источника питания). В процессе измерений записывают расстояние /, на которое сдвинулась окрашенная граница, и время т, за которое произошел сдвиг. Электрокине- тический потенциал вычисляют по уравнению Гельмгольца — Смолухов- ского, записанному относительно электрокинетического потенциала:
где отношение //т представляет собой скорость электрофореза v, м/с; напряженность внешнего поля ?вн, В/м, задается приложенным напряжением (разностью потенциалов на электродах) U, В, и расстоянием между ними L, м, Еш = U/L. Расстояние между электродами измеряют следующим образом: располагают нитку от конца одного электрода до другого вдоль U-образной трубки и затем измеряют ее длину, приложив нитку к линейке.
Приготовление исходных золей.
Золь берлинской лазури (-): 1,5 мл насыщенного раствора желтой кровяной соли K4[Fe(CN)6] разбавляют водой до 300 мл. К разбавленному раствору добавляют при перемешивании 2—3 капли насыщенного раствора FeCl3. Образуется прозрачный золь берлинской лазури FeK|Fe(CN)6|3 интенсивного синего цвета.
Золь берлинской лазури ( + ): 0,3 мл насыщенного (47%) раствора FeCl3 разбавляют водой до 300 мл. В разбавленный раствор при перемешивании вводят 2—3 капли насыщенного (20%) раствора желтой кровяной соли K4[Fe(CN)6]. Образуется прозрачный золь берлинской лазури FeK[Fe(CN)6]3 интенсивного синего цвета.
Приготовление золей с добавлением электролита
Для приготовления золя с заданным содержанием электролита Сэл к 50 мл исходного золя добавляют рассчитанный объем раствора электролита исходной концентрацией С®л (обычно добавляют NaCl с концентрацией С®л= 0,01 М). Для вычисления добавляемого объема Удоб следует воспользоваться формулой
В ходе работы проводят измерение электрокинетического потенциала исходного золя и золя с добавлением электролита.
Полученные данные записывают в таблицу (табл. Л.4).
Данные для расчета ^-потенциала золя методом электрофореза
Концентрация электролита Сэл, моль/л
источник
Тема: Электрокинетический потенциал и методы его определения
Электрокинетические явления были открыты профессором Московского университета Ф.Ф.Рейсом в 1808г. при исследовании электролиза воды.
Явление перемещения жидкости в пористых телах под действием электрического поля получило название электроосмоса, а явление перемещения частиц – электрофореза.
В 1859г. Квинке обнаружил явление, обратное электроосмосу, т.е. при течении жидкости через пористое тело под действием перепада давлений возникает разность потенциалов. Возникновение разности потенциалов Квинке наблюдал при течении воды и водных растворов через разнообразные пористые материалы (глина, дерево, графит и др.). Это явление получило название потенциала течения (или потенциала протекания).
Количественное исследование эффекта, обратного электрофорезу, впервые было выполнено Дорном в 1878г. Он измерял возникающую разность потенциалов при седиментации частиц суспензии кварца в центробежном поле. Явление возникновения разности потенциалов при осаждении дисперсной фазы получило название потенциала седиментации (или потенциала оседания).
Таким образом, по причинно-следственным признакам электрокинетические явления в дисперсных системах делят на две группы. К первой группе относят явления, при которых относительное движение фаз обусловлено электрической разностью потенциалов; это электроосмос и электрофорез. Ко второй группе электрокинетических явлений принадлежат потенциал течения и потенциал седиментации, при которых относительное движение фаз вызывает возникновение электрической разности потенциалов.
Наибольшее практическое применение получили электрофорез и электроосмос.
Электрокинетические явления в течение длительного времени не находили объяснения. Теперь, на основании рассмотренных представлений об электрических свойствах границы раздела, причиной этих явлений можно считать существование двойного электрического слоя (ДЭС). Действительно, разноименность зарядов фаз приводит в случае неподвижного пористого тела в электрическом поле к перемещению подвижных противоионов вместе с жидкой фазой к соответствующему полюсу (одноименного с твердой фазой знака). Действие же внешней механической силы (давление) вызывает вынос подвижного заряда диффузного слоя и, следовательно, возникновение разности потенциалов. Потенциал, возникающий на плоскости скольжения при отрыве части диффузного слоя, называется электрокинетическим потенциалом или ζ-потенциалом. Дзета-потенциал, отражая свойства двойного электрического слоя, характеризует природу фаз и межфазного взаимодействия.
Из этого качественного рассмотрения видно, что действующая электрическая сила (в явлениях электроосмоса и электрофореза), равная произведению заряда на градиент потенциала, тем больше, чем больше зарядов диффузного слоя оказывается в подвижной части жидкости. От этих зарядов зависит и величина конвективного тока и, следовательно величины потенциалов течения и оседания.
Таким образом, все эти явлении должны быть развиты тем сильнее, чем больше подвижный заряд диффузного слоя и ζ-потенциал границы скольжения. Отсюда следует, что ζ-потенциал есть мера интенсивности элетрокинетических явлений. С другой стороны, измеряя параметры этих явлений, можно вычислить ζ-потенциал на основе теории, связывающей его с этими параметрами.
Рис. 1. Изменение потенциала ψ и скорости u с расстоянием от поверхности.
Рассмотрим бесконечно тонкий слой жидкости толщиной dx (δ
Электрическая сила действует на отдельные ионы, но, согласно закону Ньютона, она уравновешивается силой трения, возникающей в жидкости. Таким образом, в стационарном состоянии и в ламинарном режиме суммарная сила, действующая на каждый слой, равна нулю и каждый слой жидкости толщиной dx движется с постоянной скоростью параллельно границе скольжения. Это означает, что электрическая сила, действующая на объемный заряд, должна уравновешиваться силами трения соседних слоев, равными η (du/dx), на единицу площади боковой поверхности
где ρ – объемная плотность заряда; η – коэффициент вязкости; u – линейная скорость движения жидкости.
Исходя из принципа суперпозиции полей и учитывая уравнение Пуассона
В результате интегрирования, выполняемого при граничных условиях
где uэо – электроосмотическая скорость; знак минус означает, что жидкость движется против поля, если ζ > 0
где R – сопротивление; к – удельная электропроводность жидкости; l и A – эффективные длина и площадь сечения пор.
Подстановка значений uэо и Х в уравнение (3) дает:
Это уравнение носит название уравнения Гельмгольца – Смолуховского для электроосмоса.
Таким образом, движение ионов диффузного слоя под действием электрического поля увлекает вследствие внутреннего трения всю массу жидкости, которая заполняет капилляры или поры, со скоростью Q в направлении поля.
Весьма существенно, что уравнение (5) не включает геометрических параметров системы (l, A); все величины, входящие в правую часть уравнения, измеримы на опыте. Зависимость Q от I, изученная экспериментально для многих систем, оказалась линейной, подтверждая уравнение (5).
Таким образом, экспериментальное определение Q и I позволяет вычислить ζ-потенциал.
Рис. 2. Прибор для измерения электроосмоса в мембранах.
Для измерений применяют установки различного типа; пример одной из них приведен на рис. 2. Пористая мембрана 1, зажатая между фланцами 2 и 3, разделяет два симметричных сосуда 4 с отсчетными капиллярными трубками 5 и неполяризующими электродами (Сu/CuSO4 – агар) 6. Ячейку заполняют раствором электролита так, чтобы мениски жидкости находились в средней части градуированных трубок. Соединяя электроды с внешним источником тока, измеряют объем V жидкости, перемещающийся за время t в капиллярных трубках вследствие электроосмоса в мембране 1. Для расчетов используют среднее значение скорости Qср = (V + V’)2t, нивелируя таким образом изменения V, связанные с тепловым расширением. Измерения повторяют несколько раз, меняя направление тока. Значение I среднее за период измерения определяют по амперметру, а значения η, ε и к берут из таблиц. При выполнении измерений необходимо, чтобы уровни жидкости находились на одной высоте; это исключает влияние гидростатического давления.
Можно проводить опыт по-иному, предоставив жидкости подниматься в одном из колен сосуда. В этом случае установится равновесие, в котором электрическая сила равна гидростатической (весу столба жидкости). Используя выражения (3) и (4) и формулу Пуазейля:
где Q – расход жидкости (поток) в единицу времени; Р – дпаление; r и l- радиус и длина капилляра; К – константа, определяемая геометрическими параметрами, получаем:
Измеряя равновесную высоту поднятия h, и, следовательно, гидростатическое давление P = gdh, можно найти ζ, если известен радиус пор r.
Движение частиц дисперсной фазы в постоянном электрическом поле в жидкой среде схематически изображено на рис. 3.
Рис. 3. Схема электрофореза
Отрицательно заряженная частица вместе с плотным слоем ионов внешней обкладки приобретает направленное движение в сторону положительного полюса, тогда как ионная атмосфера (диффузный слой) перемещается в противоположном направлении. При выборе системы координат, неподвижно связанной с частицей, получается картина, принципиально идентичная электроосмосу, и, следовательно, уравнение (3) должно быть применимым к электрофорезу (с обратным знаком). В отличие от электроосмоса здесь можно непосредственно измерить линейную скорость движения частиц u, а также поле X = E/l, гдн E – разность потенциалов на электродах; l – расстояние между ними.
источник
Значение ^-потенциала можно вычислить по уравнению (VII, 44). Для этого необходимо измерить скорость электрофоре — тического передвижения частиц в системе при известном градиенте потенциала прилагаемого напряжения и знать значения вязкости и диэлектрической проницаемости жидкости.
Рис. VII, 20. Влияние концентрации с электролита в растворе ка электрокинетические свойства системы: / — изменение диэлектрической проницаемости е; 2— изменение ^-потенциала, вычисленного без учета изменения е; 3— изменение £-потенциала, вычисленного с учетом изменения е; 4—изменение электрофоретической подвижности и.
Однако прежде чем рассматривать экспериментальные методы определения скорости электрофоретического переноса, остановимся на различного рода ограничениях, которые надо иметь в виду при применении уравнений (VII, 42) и (VII, 44).
Согласно исходным положениям, электрофорез представляет собой явление, близкое электроосмосу. И для электрофореза, и «для электроосмоса, как мы приняли ранее, перемещение жидкости по отношению к поверхности твердой фазы определяется силами, действующими на двойной электрический слой. Именно исходя из этих предпосылок нами и было выведено уравнение Гельмгольца — Смолуховского, выражающее зависимость скорости электрофореза от градиента потенциала внешнего поля. Однако применение уравнения (VII, 42) для описания электрофоретических явлений ограничено следующими условиями. Во-первых, толщина двойного слоя (обычно характеризуемая величиной 1/х) должна быть мала по сравнению с размером частицы. Во-вторых, вещество частицы не должно проводить электричества, а поверхностная проводимость на межфазной границе должна быть настолько малой, чтобы она практически не влияла на распределение внешнего электрического поля.
Длительное время уравнение Гельмгольца — Смолуховского считали справедливым во всех случаях, независимо от того, выполняются ли вышеприведенные условия или нет. Но в 1924 г. Гюк — кель, основываясь на новой теории сильных ‘электролитов, дал другое уравнение, отличающееся от уравнения (VII, 42) численным множителем 2/з:
При выводе этого уравнения коллоидная частица принята эквивалентной сферической частице и введена поправка на так называемое электрофоретическое^ запаздывание (торможение), вызванное влиянием внешнего поля на двойной электрический слой. Под действием этого поля противоионы передвигаются в направлении, противоположном движению частицы, сообщая этим самым движение окружающей жидкости в том же направлении. Это приводит к тому, что частица перемещается не в покоящейся, а в движущейся жидкости, в результа. те чего электрофоретическая скорость уменьшается.
Генри в 1931 г. показал, что уравнения (VII, 42) и (VII, 47) справедливы каждое в отдельном случае. При выводе уравнения (VII, 42) учитывалась деформация электрического поля, вызванная непроводящей частицей, а при выводе уравнения (VII, 47) допускалось, что непроводящие частицы не влияют на поле в двойном слое и объеме жидкости. Последнее предположение справедливо лишь тогда, когда электропроводность частиц равна электропроводности среды или размеры частиц так малы по сравнению с толщиной двойного слоя, что деформация в большей части двойного слоя становится несущественной.
Тщательно рассматривая вопрос с математической точки зрения и принимая во внимание деформацию внешнего поля, Генри показал, что ^скорость электрофореза во всех случаях может быть выражена уравнением
Где f^ функция величины ха; а — радиус сферической частицы или длинная ось цилиндрической Частицы; и— величИна, обратная толщине двойного слоя, численно равная */ъпегЫА £ czVbkT.
Значение величины F неодинаково для частиц разной формы и различно расположенных по отношению к полю. Зависимость этой величины от ха показана на рис. VII, 21.
Для непроводящих цилиндрических частиц, ось которых совпадает с направлением поля, /= 1/4, как в уравнении (VII, 42). Для цилиндрических частиц, расположенных перпендикулярно направлению поля, F — 1/8 при малых значениях ха в приближается к 1/4 прн больших величинах ха. Для сферических
Частиц F = 1/6 при малых значениях ш и F «= 1/4 при больших значениях этой величины. Таким образом, данные рис. VII, 21 находятся в полном соответствии с уравнением (VII, 42), согласно которому численный коэффициент равен 1/4 независимо от формы частиц, если значение ха велико, н с уравнением (VII, 47), согласно которому численный множитель равен 1/6 для сферических частнц с малым значением на.
Геири проанализировал также влияние на величину F электропроводности дисперсной фазы, полностью меняющей распределение электрического поля вблизи частиц. На рис. VII, 21 пунктиром обозначены значения коэффициента f в зависимости от величины ха для электропроводящих частиц сферической формы. Как и следовало ожидать, распределение поля ве сказывается на величине F при очень большой толщине двойного электрического слоя (Ха
Таким образом, объем жидкости, электроосмотически перенесенной через мембрану, прямо пропорционален поперечному сечению капилляров, диэлектрической проницаемости, ^-потенциалу, приложенной электродвижущей силе и обратно пропорционален вязкости жидкости.
Где Е — приложенная разность потенциалов; I — сила тока; R — электрическое сопротивление системы. Электрическое сопротивление раствора электролита равно: — .
Где L — толщина слоя раствора; S — площадь сече — стационарного режима ния; у —удельная электмпооводиость раствора. Под — течения жидкости в ка — ставляя в уравнение (VII, 53) приведеииое выраже — пилляре:
НИЄ для R, получим: о—при электроосмосе; в—под
IL ,,„, „. действием гидростатического
Подставляя найденное значение градиента в уравнение (VII,52), имеем:
Так как в уравнение (VII, 57) не входит ии L, ии S, то, очевидно, при постоянной силе тока объем жидкости, прошедший сквозь мембрану, ие зависит от поперечного сечения и длины капилляров. Правильность уравнения (VII, 57) была подтверждена опытами Видемана.
Из уравнения (VII, 57) легко найти значение С-потеициала:
По аналогии с уравнением (VII, 46) правую часть этого уравнения надо умножить на 3002 для того, чтобы ^-потенциал был выражен в вольтах. Тогда уравнение (VII, 58) будет иметь вид:
Таким образом, для того чтобы определить значение J-потенциала по электроосмосу, следует экспериментально определить объем жидкости, перенесенной
•через капилляр или пористую мембрану, удельную электропроводность раствора и силу тока, при которой проводился электроосмос. Остальные величины берут -обычно из справочников.
При использовании уравнения (VII, 58) необходимо учитывать возможность явления так называемой поверхностной проводимости. Это явление сводится к тому, что находящиеся около межфазной границы ионы изменяют состав среды, а следовательно, и удельную электропроводность раствора у межфазиой границы. Если радиус капилляра достаточно велик по сравнению с толщиной слоя у стенки, где проявляется поверхностная проводимость, средняя электропроводность раствора остается приблизительно той же, что и в его объеме, и вели — «чина у в уравнении (VII, 58) является удельной электропроводностью раствора.
Рис. VII, 30. Зависимость ^-потенциала от радиуса капилляра г С учетом (/) н без учета (2) поверхностной проводимости: Л—мембрана нз кварца; 5—мембрана нз корунда.
ТЗсли же капилляры тонкие, это условие не соблюдается и у становится уже функцией радиуса капилляра. В этом случае вместо уравнения (VII, 58) следует .пользоваться уравнением:
•где О — длина окружности капилляра; s — его сечение; у*— поверхностная проводимость.
Множитель (у + Oy>/S) в числителе уравнения (VII, 60) ставится вместо величины у. исходя из следующих соображений. Электропроводность жидкости, заполняющей капилляр, Y равна сумме электропроводностей (обратных сопротивлений) объемной части жидкости и приповерхностного слоя:
Где 1IR = Ys/L, L/R — Ys/L и L/R, = Ys O/L, причем принимается, что толщина слоя с поверхностной проводимостью мала по сравнению с радиусом капилляра. Отсюда общая электропроводность у равна
Величина Ov’s/s, очевидно, представляет собой увеличение электропроводно — — сти жидкости в капилляре в результате поверхностной проводимости. Так как O/S
1/г, то поправка на поверхностную проводимость не нужна при капиллярах достаточно большого радиуса.
Сравнивая уравнения (VII, 58) и (VII, 60) и учитывая, что величина Oys/S Всегда положительна, можно видеть, что вследствие поверхностной проводимости истинные значения С-потенциала при достаточно тонких капиллярах всегда выше вычисленных без введения поправки на поверхностную проводимость. Эксперименты подтвердили это положение. На рис. VII, 30 приведены резуль — тэты опытов И. И. Жукова по определению С-потенциала протекания, вычисленные с учетом (кривые 1) и без учета (кривые 2) поверхностной проводимости. В качестве пористых мембран были взяты диафрагмы из кварца и корунда, в качестве жидкости — слабый раствор хлорида калия. По характеру кривых видно, что значения С-потенциала без учета поверхностной проводимости сильно уменьшаются при переходе к диафрагмам с порами малого сечения, а при введении поправки иа поверхностную проводимость получаются почти одни и те же — значения электрокинетического потенциала во всем испытанном диапазоне радиусов капилляров. Следовательно, при определении С-потенциала электроосмотическим путем нли методом протекания необходимо всегда учитывать радиус пор- капилляров.
Приведенная выше поправка характеризует поверхностную проводимость только отдельного капилляра, тогда как на практике в большинстве случаев, реальными объектами являются пориыые тела. Для определения поправки на
Рис. VII, 31. Схема прибора Перрена для электроосмоса:
1 — порошок исследуемого вещества; 2— электроды; 3— вороика; 4 — кран;
5 — прокалиброванная трубка.
Поверхностную проводимость пористых тел измеряют электросопротивление — мембраны в исследуемом и стандартном растворах и по этим данным вычисляют величину Ys-
С поверхностной проводимостью связано явление так называемой капиллярной сверхпроводимости. Это явление, открытое Д. А. Фридрихсбергом, заключается в следующем. Если трубку с проводящим ток раствором перегородить пористой диафрагмой из непроводящего материала, то электрическое сопротивление системы должно возрасти вследствие того, что часть сечения трубки будет занята диэлектриком. Однако если у поверхности капилляров диафрагмы образуется слой, обладающий поверхностной проводимостью, то за счет этой проводимости для весьма тонкокапиллярных пористых тел в разбавленных растворах электролитов может наблюдаться повышение общей проводимости. Будет иметь место на первый взгляд парадоксальный эффект понижения электрического сопротивления при введении в трубку диафрагмы из диэлектрика.
Остановимся теперь кратко на приборах, применяемых для определения С-потенциала по объему электроосмотически перенесенной жидкости. Во всех приборах этого типа электроосмос проводится не с одиночным капилляром, а с помощью пористой диафрагмы из твердого вещества.
На рис. VII, 31 приведена схема прибора для электроосмоса, предложенного еще Перреном. В среднюю часть стеклянной U-образной трубки, присоединяемой к боковым коленам с помощью шлифов, набивают достаточно плотно порошок 1 исследуемого вещества. В оба боковых колена вставлены платиновые электроды 2, питаемые постоянным током, напряжение которого должно составлять не менее 40—50В. В правом боковом колене имеется воронка 3 с краном для заполнения прибора дисперсионной средой, а в левом колене — кран 4 для слива
жидкости из прибора. Кроме того, к правому колену трубки присоединена капиллярная горизонтальная заранее прокалиброванная трубка 5, служащая для наблюдения за перемещением в ней жидкости.
Перед определением прибор заполняют жидкостью так, чтобы в порах диафрагмы / не оставалось воздуха и установилось постоянное положение мениска жидкости в левой части капиллярной трубки 5. После этого включают ток в таком направлении, чтобы мениск в капилляре 5 передвигался слева направо, и отсчитывают скорость его перемещения по секундомеру. Одновременно с помощью миллиамперметра, включенного в электрическую цепь прибора, измеряют силу тока. Недостатком прибора является поляризация электродов и образование продуктов электролиза, которые могут проникать в капилляры диафрагмы и этим самым вносить ошибку в результаты измерения.
В’ более совершенных приборах применяют иеполяризующиеся электроды, достаточно удаленные от диафрагмы или соединенные с ней с помощью агаровых мостиков. В приборе для электроосмоса, предложенном Уметсу, диафрагма из порошка располагается в вертикальной стеклянной трубке со стеклянной решеткой в нижней ее части.
Диафрагму необходимой высоты получают, наполняя трубку суспензией порошка н отсасывая затем жидкость водоструйным насосом. После этого прибор заполняют раствором, вставляют агаровые мостики для соединения диафрагмы с неполяризующимися электродами и включают постоянный электрический ток. Скорость электроосмоса определяют с помощью калиброванного стеклянного капилляра, при этом начальное положение мениска жидкости устанавливают, приоткрывая специальный боковой кран.
Определение по электроосмотическому давлению. При этом способе определяют не объем жидкости, протекшей при электроосмосе через капилляр или пористую мембрану в единицу времени, а давление, возникающее в результате электроосмотического движения жидкости. Для этого то колено электроосмотического прибора, в которое поступает жидкость, должно заканчиваться вертикальной или наклонной трубкой, с помощью которой можно установить высоту столба жидкости, уравновешивающего электроосмотическую силу. Давление этого столба заставляет жидкость течь через капилляр или пористую мембрану в обратном направлении, пока не установится равновесие между-силой тяжести и ■осмотическим давлением.
Уравнение, с помощью которого можно вычислить С-потенциал, выводят, исходя из того, что в равновесном состоянии объем жидкости Vi, поступающей в отдельный капилляр в единицу времени под влиянием электроосмотической силы, равен объему жидкости V2, вытекающему за то же время из капилляра под влиянием гидростатического давления Р. Объем Vi выражается уравнением (VII, 51):
Для Vi, согласно уравнению Пуазейля, можно написать:
В равновесном состоянии Vt = V2 и, следовательно:
Еще Квинке и Видеман нашлн, что электроосмотическое давление Р пропорционально градиенту внешнего потенциала Н и обратно пропорционально гг, что полностью соответствует уравнению (VII, 64).
Из уравнения (VII, 64) легко иайти значение С-потеициала по давлению Р или высоте поднятия жидкости в трубке.
Подобный метод можно применить (в отсутствие поверхностной проводимости) также и при электроосмосе через пористую мембрану. Однако он не получил широкого распространения иа практике.
Из изложенного выше ясно, что определение электрокинетического потенциала сопряжено со многими трудностями, связанными как с постановкой эксперимента, так и с вычислением ^-потенциала по экспериментальным. данным. Еще сравнительно недавно исследователи не учитывали влияния поверхностной проводимости, электрофоретиче — ского запаздывания и электрической релаксации, и поэтому нз большого числа исследований в области электрокннети — ческих явлений лишь немногие давали достоверные значения ^-потенциала.
Наилучшим доказательством точности значений £-по — тенциала, определяемых с учетом нужных поправок, может служит^ идентичность его значений, найденных при различных электрокинетических явлениях.
Опыты, проведенные Рат — джерсом, а также Вьигом с целью сравнения значений ^-потенциала, определенного методом протекания и по электроосмвсу, показали одинаковость этих значений. На рис. VII, 32 представлена зависимость между £-потен — циалом стенки стеклянного капилляра и концентрацией раствора электролита, заполняющей» капилляр. Как можно видеть, значения ^-потенциала, вычисленные из электроосмотических данных и из данных, полученных при определении потенциала протекания, ложатся на одну и ту же кривую. Расхождения данных для KNOj объясняются другой обработкой капилляра, примененного в этом опыте.
Концентрации электролита: 1—данные, вычисленные по реаультатам электроосмотических определенна; 2—данные, полученные прн определения потенциалов течения.
Эквивалентность значений ^-потенциала, найденных с помощью электрофореза и электроосмоса, также неоднократно проверялась. В частности, Абрамсон в своих тщательных опытах по исследованию электроосмоса и микроэлектрофореза покрытых белком частиц при учете всех необходимых поправок установил равенство
значений ^-потенциала, найденных обоими способами. Наконец, ^-потенциал, определенный по методу протекания, оказался равным ^-потенциалу, вычисленному из электрофоретических данных.
Таким образом, хотя экспериментальный материал не очень велик и не всегда является абсолютно доказательным, тем не ме — Знее можно утверждать, что все три электрокинетические явления эквивалентны и значения ^-потенциала, определенные этими тремя методами, одинаковы.
источник
Направленное перемещение частиц дисперсной фазы под действием электрического поля может наблюдаться в седиментационно-устойчивых дисперсных системах. При этом происходит разрыв ДЭС по плоскости скольжения, в результате частица приобретает определенный заряд и движется к соответствующему электроду.

Рис. 18. Схема движения коллоидных частиц в электрическом поле.
Линейная скорость (U) – движение частиц относительно мембраны при электроосмосе и движение частиц при электрофорезе:
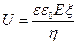
где 
При движении частиц дисперсной фазы они вынуждены взаимодействовать с противоионами дисперсионной среды, что вызывает электрофоретическое торможение, что уменьшает линейную скорость при электрофорезе.
Электрофоретическое торможение 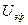
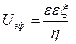
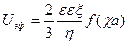
где f — параметр Дебая, α – диаметр частицы. Единицы измерения электрофоретического торможения 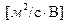
Характеристикой электрофореза является также электрофоретическая подвижность, которая характеризует электрофоретические свойства системы без учета влияния внешнего электрического поля и служит для сравнения способности к электрофорезу различных коллоидных систем.
При исследовании явления электроосмоса для практического применения при расчете электрокинетического потенциала удобнее использовать уравнение, в которое входят величины, измеряемые экспериментально. Выразим линейную скорость через объёмную:
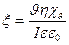
где r – радиус капилляра, l – длина капилляра, I – сила тока, ρ – удельное сопротивление, χv – удельная электрическая проницаемость жидкости, R – сопротивление.
Пи расчете электрокинетического потенциала и при выборе оптимального режима ряда технологических процессов (проведение электродиализа, определении пористости грунтов т.д.) необходимо учитывать поверхностную проводимость χs – это явление сводится к тому, что находящиеся около межфазной границы ионы изменяют состав среды, они являются причиной передвижения жидкости или частиц. Изменение состава среды ведёт к изменению электропроводности раствора у межфазной границы.
Поверхностная проводимость χs учитывается путём введения коэффициента эффективности диафрагмы α:
Путём электроосмоса удаляют влагу из капиллярнопористых систем и понижают уровень грунтовых вод при возведении гидротехнических сооружений.
Метод электрофореза применяют для формирования изделий из тонких взвей последующим спеканием для разделения, выделения и исследования биоколлоидов, особенно белков.
Возникновение электрических полей при течении грунтовых вод помогает в геологической разведке полезных ископаемых и водных источников.
источник
Электрокинетические явления и причины их возникновения.
Электрокинетические явления были открыты профессором Московского университета Ф.Ф.Рейсом в 1808 г. Рейс исследовал явление электролиза воды (недавно открытое Фарадеем).
Электроосмос– явление перемещения жидкой дисперсионной среды относительно неподвижной дисперсной фазы под действием электрического поля.
Электрофорез – явление перемещения дисперсной фазы относительно жидкой дисперсионной среды под действием электрического поля.
Потенциал течения – возникновение разности потенциалов при движении дисперсионной среды относительно неподвижной дисперсной фазы.
Потенциал оседания (седиментации) – возникновение разности потенциалов при движении дисперсной
фазы относительно дисперсионной среды.
Электрокинетическими явления – это явления, в которых существует связь между скоростью протекания (кинетикой) и электрическим полем.
Причиной электрокинетических явлений является наличие на границе раздела фаз двойного электрического слоя (ДЭС).
Электрокинетический потенциал и методы его определения.
Электрокинетический (дзета) потенциал – потенциал, возникающий на границе скольжения фаз при их относительном перемещении в электрическом поле. Электрокинетический потенциал отражает свойства ДЭС и определяется экспериментально из электрокинетических явлений.
Электрокинетический потенциал является важнейшей характеристикой коллоидной системы, ее двойного электрического слоя, поскольку он не зависит от параметров системы, в которой находится золь (радиус, длина, форма пор диафрагмы). Электрокинетический потенциал является однозначной характеристикой электрических свойств данной границы раздела и определяется экспериментально из электрокинетических явлений, связанных с относительным перемещением фаз. Порядок величин ζ в зависимости от состава фаз и концентрации электролита обычно составляет 0,01÷0,1 В.
Скорость, как электрофореза, так и электроосмоса, при постоянной разности потенциалов пропорциональна величине ζ потенциала. Поэтому, определяя скорость перемещения заряженных частиц или скорость перемещения жидкости, можно вычислить величину электрокинетического потенциала.
Скорость перемещения коллоидной частицы в электрическом поле зависит:
— от свойств дисперсионной среды (вязкости η, диэлектрической проницаемости ε);
— от строения ДЭС коллоидной частицы — величины ζ,
— напряженности внешнего электрического поля Н.
Электрофоретической (электроосмотической) подвижностью (U0):
U
где U0 – электрофоретическая подвижность, м2/В·с; U – линейная скорость движения границы золь – боковая жидкость, м/с; H – напряженность электрического поля, В/м.
Электрокинетический потенциал связан с электрофоретической (электроосмотической) подвижностью, уравнением Гельмгольца – Смолуховского:
где ζ – величина электрокинетического потенциала, В; η – вязкость среды, Н·с/м2; ε – диэлектрическая проницаемость среды, для водной среды равная 81 (безразмерная величина);

Линейную скорость движения границы золь:
где h – смещение границы золь — боковая жидкость за время элетрофореза, м; t – время электрофореза, с.
Напряженность электрического поля (градиент потенциала) расчитывают как отношение приложенной разности потенциалов к растоянию между электродами:
где Е – приложенная разность потенциалов, В; l – расстояние между электродами, м.
Тогда уравнение Гельмгольца — Смолуховского для электрофореза запишется:
studopedia.org — Студопедия.Орг — 2014-2019 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.002 с) .
источник

